PT・OT国家試験では論文を読むために必要な尺度や統計の知識を問われることがあります.あまり馴染みがないため,受験生にとっては苦手な分野の1つになっています.
ここではPT・OT国家試験で出題される尺度や統計について解説します.
尺度
尺度は名義尺度・順位尺度・間隔尺度・比例尺度の4つに分類されます.これらの相違を理解していれば国家試験は問題ありません.
名義尺度
同一性の情報を他と区別する尺度です.例えば,血液型を(1.A型 ・ 2.B型 ・ 3.O型 ・ 4.AB型)区別する,性別を(1.男性 ・ 2.女性)区別する,転倒歴が(1.ある ・ 2.ない)を区別するように情報を区別するために用いられます.
区別を目的にしているので,数値の大小に意味はありません(A型は1でO型は3なのでO型の方が大きい…これは成り立ちません).
順位尺度
同一性に加え,順位を決める尺度です.例えば模試結果を(1位Aさん,2位Bさん,3位Cさん…)のように順位を決めて情報を区別するために用いられます.順位を決定することはできますが,順位間の距離(例えばAさんとBさんの点数差とBさんとCさんの点数差)は一定ではありません.
間隔尺度
同一性,順位性に加え,数値間の距離が等間隔の尺度です.そして基準となる0を1つに定めることができません.そのため加減(足し算・引き算)は可能ですが,乗除(掛け算・割り算)はできません.
比例尺度
同一性,順位性に加え,数値間の距離が等間隔で,基準となる0を1つに定めることができる尺度です.そのため加減乗除(足し算・引き算・掛け算・割り算)が可能です.
間隔尺度と比例尺度の区別に迷うはずです.間隔尺度と比例尺度を区別は0が存在するかor存在しないかで判断します.
例えば知能検査の結果,IQが0点の人の知能は存在します.また,気温0℃も存在するし,西暦0年も存在します.このように数値が0でも存在する場合は間隔尺度です.
一方で体重0kgや身長0cmは存在しません(無です).このように数値は0が存在しない(存在が無い)場合は比例尺度です.
具体例
| 尺度 | 評価名 | |
| 質的データ | 名義尺度 | 性別,血液型,疾患名など |
| 順位尺度 | MMT,BRS,Barthel Indexなど | |
| 量的データ | 間隔尺度 | IQ,VASなど |
| 比例尺度 | 身長,体重,ROM,握力など | |
ココがポイント
4つの尺度の情報量は名義尺度→順位尺度→間隔尺度→比例尺度の順に大きくなります.
さらに詳しく知りたい方は↓
-

-
質的データを攻略|名義尺度と順位尺度
根拠に基づいた理学療法や作業療法を実施するためには最新の知見を入手しなければなりません.インターネットの普及により,以前に比べ情報へのアクセスは容易になりました.しかし,入手した情報(論 ...
続きを見る
-

-
量的データを攻略|間隔尺度と比例尺度
入手した論文を理解するために,統計学の知識を身につけましょう.ここでは量的尺度(間隔尺度と比例尺度)を再学習したいと思います. 前回のおさらいも合わせてどうぞ. 量的尺度 間隔尺度 順位 ...
続きを見る
検定
検定(統計手法)にはたくさんの種類があります.条件に合わせて適切な検定を選択しなければなりません.適切な検定を選択するために,まず得られたデータがパラメトリック法になるか,またはノンパラメトリック法になるかを確認する必要があります.
パラメトリック法とノンパラメトリック法
パラメトリック法はデータ尺度が間隔尺度・比例尺度で正規分布に従う場合に使用します.
ノンパラメトリック法はデータ尺度が順位尺度・間隔尺度・比例尺度で正規分布に従わない場合に使用します.
データの正規性を判断するためには,シャピロ・ウイルク(Shapiro-Wilk)検定を使用して正規分布するか否かを判定します.
相関の検定
勉強時間が多い学生はテストの点数が良い,筋肉量が多いほど握力が強いなど変数間の関連性を相関(勉強時間とテストの点数,筋肉量と握力)といいます.
2変量の間に関係の有無を判定する方法には,ピアソンの積率相関係数とスピアマンの順位相関係数があります.ピアソンの相関係数はパラメトリック法,スピアマンの相関係数はノンパラメトリック法の相関係数になります.
差の検定
2つ以上のデータ間に「差がある」or「差がない」を判断するために差の検定を行います.検定の選択にはパラメトリック法orノンパラメトリック法の確認のほかに,もう1つ確認することがあります.それはデータの対応の有無の確認です.
対応のあるorないデータとは?
例 ①:新薬の効果を判定するために,服用前と服用後の血圧データに差があるかorないかを検定する場合…
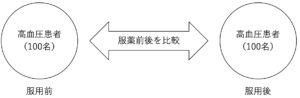
新薬服用前と服用後の被験者は同一の人(同一グループ)です.このようなデータを対応のあるデータと呼びます.
例 ②:東京の高齢者と大阪の高齢者の血圧に差があるか(地域差)を検定する場合…
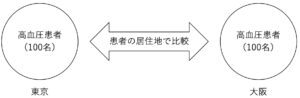
東京の高齢者と大阪の被験者は別々の人(別グループ)です.このようなデータを対応のないデータでと呼びます.
検定の種類
差の検定の有無を判定する方法にはt検定,ウェルチの検定,ウィルコクソンの符号付き順位検定,マン・ホイットニーの検定があります.
| パラメトリック法 | ノンパラメトリック法 | |
| 対応のある差(2変量) | 対応のあるt検定 | ウィルコクソンの符号付き順位検定 |
| 対応のなり差(2標本) | 対応のないt検定 ウェルチの検定 | マン・ホイットニーの検定 |
パラメトリックorノンパラメトリック,対応の有無により検定が異なるので注意が必要です!
ココに注意
データが名義尺度の相違を調べる場合はカイ2乗検定(χ2)を使用します.
参考文献
・石川朗ほか:リハビリテーション統計学.中山書店.
・山田孝:作業療法研究法.医学書院.