対象者(サンプルサイズ)が増えると必然的にデータも増えます.データが多くなると,集団の特性の把握が困難になります.そのため集団の特性を理解するために,代表値を利用することがあります.ここでは,代表値について説明します.
代表値
代表値とは,データの中心を示す値です.代表値には,平均値,中央値,最頻値があります.
平均値(Mean)
平均値はデータの平均です.平均値は全てのデータを足して,データ数で割った値です.
例としてテスト結果を示します.
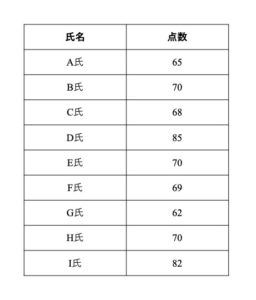
この表をもとに平均値を求めると,(65+70+68+85+70+69+62+70+82) / 9 = 71.222...になります.
テストなどは間隔尺度なので加法が可能でしたね.この平均値は馴染みがあると思います.
中央値(median)
データを大きさの順(小→大または大→小)に並べ,ちょうど真ん中(中央)に位置する値が中央値です.
62,65,68,69,70,70,70,82,85
この表は9人分のデータなので,小さい方から数えて5番目(大きい方から数えて5番目)が中央値(70点)になります.データ数が多くなった場合は,(データ数+1)/ 2を計算することにより中央値の順番が分かります.
ここでは,データ数が9なので(9+1)/ 2 =5となり5番目の値が中央値になります.
ココに注意
データ数が奇数の場合は,ちょうど真ん中になる数字は1つに定まりますが,偶数の場合はちょうど真ん中になる数字はありません.データが偶数の場合は,中心にある2つのデータを平均した値が中央値になります.
最頻値(mode)
データ中で最も出現する頻度の高い値が最頻値です.
65,70,68,85,70,82,62,70,82
ここでは,70点が最頻値です.
注意点
代表値は平均値を用いるのが一般的です.しかし,外れ値がある時には注意が必要です.
外れ値とは
他のデータの値から大きく外れた値.外れ値の中で,測定ミスなどの原因が分かっているものを異常値といいます.
例として先程の表にJ氏の点数を加えたテスト結果を示します.
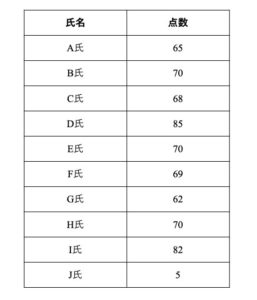
J氏の点数をミスで5点と入力したと仮定します.これらを平均すると
(65+70+68+85+70+82+62+70+82+5)/ 9 = 64.6
J氏が加わる前の71.222....に比べ平均値が大きく低下しました.
では,中央値ではどうでしょうか.
5,62,65,68,69,70,70,70,82,85
サンプルサイズが偶数になるので,中央値は(69+70)/ 2 = 69.5になります.
外れ値の影響が平均値に比べ少ないです.
最頻値もみてみましょう.
5,65,70,68,85,70,82,62,70,82
J氏が加わる前と比べても最頻値は変化していません.外れ値の影響を全く受けていないです.
このように,誤ったデータの影響を受けることが少ないことを「抵抗性(resistance)がある」といいます.
まとめ
代表値について説明しました.平均値の注意点を述べましたが,中央値や最頻値にもメリットとデメリットがあります.得られたデータから何を把握したいのかによって,どの代表値を使用するか選択する必要があります.
参考文献
・関屋曻:真に役立つ研究のデザインと統計処理.三輪書店.
・川端一光ほか:心理学のための統計学入門.誠信書房.
・石川朗ほか:15レクチャーシリーズ リハビリテーション統計学.中山書店.
