分散｜データの散らばりを把握しよう！

集団の特性を理解するためにデータの散らばりを把握する必要があります．今回はデータのばらつきを示す散布度の1つである分散（variance）を説明します．

代表値についてはこちら↓

代表値での比較

運動学と生理学のテスト結果を示します．運動学の点数は70点代でまとまっている感じがします．一方で生理学は得点の開きが大きいような印象を受けます．2つの結果を比べてみましょう．

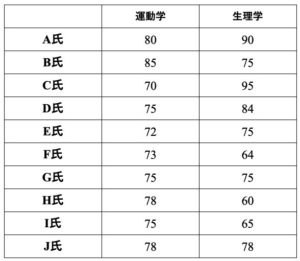
代表値

代表値の結果を示します．

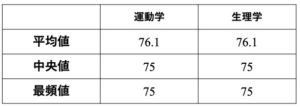
代表値は全て同じです．生理学の得点の開きを代表値では示すことができないようです．

分布図

次に点数分布の図を示します．

運動学は中心にデータが集まっています．一方，生理学は全体的にデータが散らばっています（中心から離れているデータが多い）．代表値が同じでも，データ分布の散らばりの程度が異なっています．

上記のように集団の特性を把握するために，データの散らばりも理解する必要があります．データの散らばりの程度を数値として示したものを散布度（measure of dispersion）といいます．散布度の1つに分散があります．

分散（variance）

分散はデータの散らばりの程度を示す値です．分散の計算方法を示します．

偏差を求める

分散を計算するためには，まず偏差（deviation）を求める必要があります．偏差 = データ – 平均で求めます．ここでは運動学の個人の偏差を求めます．個人の運動学の点数から運動学の平均76.1点を引いていきます．

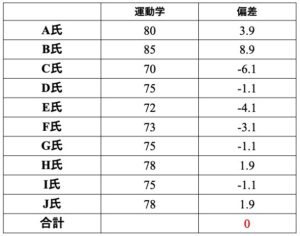
偏差の和は0になります．

偏差平方和を求める

続いて偏差を2乗します．そして全データを足します（偏差平方和）．

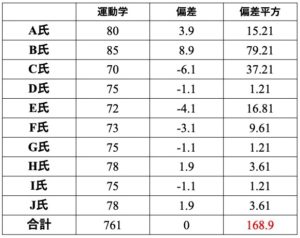
分散を求める

分散は偏差平方和をデータ数もしくはデータ数–1で割ることで計算できます．

ここでは標本分散を用いて運動学と生理学の散らばりの程度を比較します．

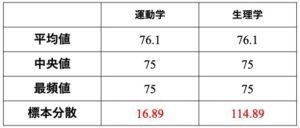
運動学と生理学の分散の値が算出されました．分散の値は0に近づけば散らばりが少ないと判断されます．運動学は生理学に比べ，データの散らばりが少ないことが数値からも分かります．

まとめ

データの散らばりの程度を確認する分散を説明しました．集団を把握するために，また標準偏差を計算するために理解する必要があります．

参考文献

・関屋曻：真に役立つ研究のデザインと統計処理．三輪書店．

・川端一光ほか：心理学のための統計学入門．誠信書房．

・石川朗ほか：15レクチャーシリーズ リハビリテーション統計学．中山書店．